Infinite Square Well

슈뢰딩거 방정식을 무한 사각형 우물 형태의 퍼텐셜에서 푸는 것은 양자역학에서 가장 기본적인 예제 중 하나입니다. 구체적으로 퍼텐셜을 다음과 같습니다: $$ V(x) = \begin{cases} 0 & (0 \le x \le a), \\ \infty & \text{otherwise.} \end{cases} $$ 위의 퍼텐셜에 대해 시간에 무관한 슈뢰딩거 방정식 $$ - \frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2} + V\psi = E\psi $$ 을 풀어 정상상태의 파동함수를 얻을 수 있습니다: $$ \psi_n(x) = \sqrt{\frac{2}{a}}\sin\left(\frac{n\pi x}{a}\right). $$ 또한 이들의 선형결합으로부터 시간을 포함하는 일반적인 해를 얻을 수 있습니다: $$ \Psi(x,t) = \sum_{n=1}^{\infty}c_n \sqrt{\frac{2}{a}}\sin \left(\frac{n\pi x}{a}\right)e^{-iE_nt/\hbar}.\tag{1} $$ 여기서 $E_n = \frac{n^2\pi^2\hbar^2}{2ma^2}$이며 $c_n$은 $t=0$일 때의 파동함수로부터 구할 수 있습니다: $$ c_n = \sqrt{\frac{2}{a}} \int_0^a \sin\left(\frac{n\pi x}{a}\right)\Psi(x, 0)dx. $$ 여기서는 초기 파동함수 $\Psi(x, 0)$을 시간에 의존하는 슈뢰딩거 방정식 $$ i\hbar \frac{\partial\Psi}{\partial t} = - \frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial x^2}+V\Psi $$ 을 이용하여 시간에 대한 파동함수 $\Psi(x, t)$를 수치적으로 구해볼 것입니다.

Exact Solution

우리는 이미 식 (1)과 같은 정확한 해를 알고 있습니다. 이를 통해 $\Psi(x, 0)$이 $\psi_{n_1}(x)$와 $\psi_{n_2}(x)$의 선형결합으로 표현될 때, $\Psi(x, T)$를 구할 수 있습니다. 다음 코드는 그러한 $\Psi(x, 0)$와 $\Psi(x, T)$를 구하는 과정입니다. 
import matplotlib.pyplot as plt
import numpy as np

a = 1
N = 100
hbar = 1
m = 1
kappa = 1j * hbar / 2 / m
dt = 0.0001
tN = 1000
T = dt * tN

x = np.linspace(0, a, N + 1)
dx = a / N
n1 = 1
n2 = 2
Psi = 1 / np.sqrt(2) * (np.sqrt(2 / a) * np.sin(n1 * np.pi / a * x) 
                        + np.sqrt(2 / a) * np.sin(n2 * np.pi / a * x))
Psi = np.array(Psi, dtype=np.complex128)

E_1 = n1 * n1 * np.pi * np.pi * hbar * hbar / 2 / m / a / a
E_2 = n2 * n2 * np.pi * np.pi * hbar * hbar / 2 / m / a / a

Psi_sol = 1 / np.sqrt(2) * (np.sqrt(2 / a) * np.sin(n1 * np.pi / a * x) * np.exp(-1j * E_1 * T / hbar) 
                            + np.sqrt(2 / a) * np.sin(n2 * np.pi / a * x) * np.exp(-1j * E_2 * T / hbar))

plt.plot(x, np.abs(Psi) ** 2)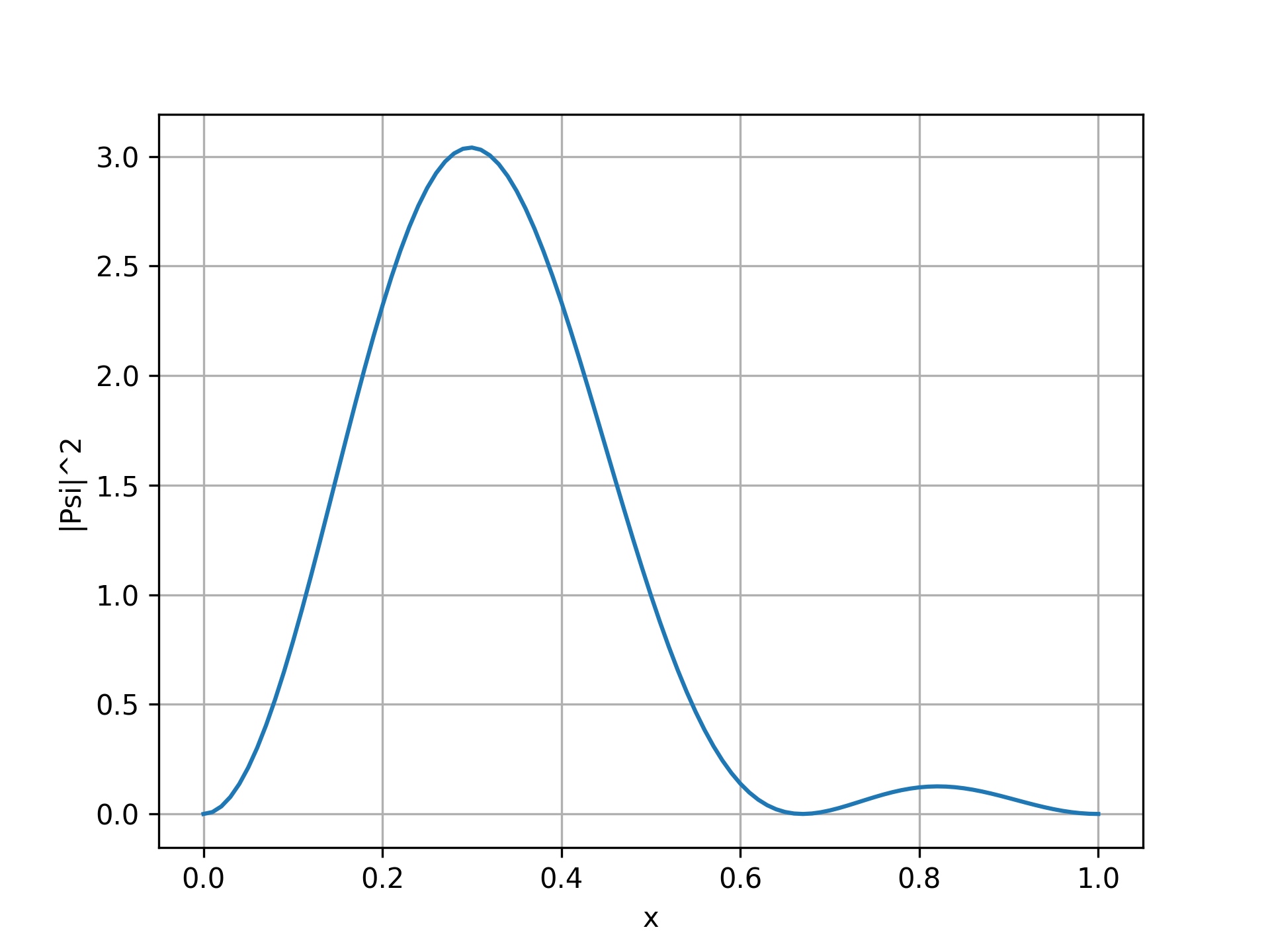
다음 그림은 $n_1=1$, $n_2=2$, $a=1$일 때 $|\Psi(x, 0)|^2$을 나타냅니다.

Time evolution

유한 차분법을 사용하여 $\Psi$를 시간에 따라 적분할 것입니다. 가장 단순한 방법은 전방-시간 중심-공간forward-time centered-space(FTCS) 방법입니다. 이는 공간에 대해선 중심 차분을 사용하고 $$ \frac{\partial^2\Psi_i}{\partial x^2} \to \frac{\Psi(x_{i+1}) - 2 \Psi(x_{i}) + \Psi(x_{i-1})}{(\Delta x)^2} + \mathcal{O}(\Delta x^2), $$ 시간에 대해선 전방 차분을 사용합니다: $$ \frac{\partial \Psi_i}{\partial t} \to \frac{\Psi_i^{n+1} - \Psi_i^{n}}{\Delta t} + \mathcal{O}(\Delta t). $$ 이는 단순하지만 안정적인 적분을 위해 $\Delta x^2$에 비례하는 매우 작은 $\Delta t$를 선택해야 한다는 문제가 있습니다.
여기서는 암묵적 차분 방법implicit differencing scheme을 사용하겠습니다. 이는 $$ \frac{\partial \Psi}{\partial t} = \kappa \frac{\partial^2 \Psi}{\partial x^2} $$ 형태의 방정식을 $$ \Psi_i^{n+1} = \Psi_i^n + \frac{\kappa \Delta t}{\Delta x^2}(\Psi^{n+1}_{i + 1} - 2\Psi^{n+1}_{i} + \Psi^{n+1}_{i - 1}) $$ 으로 적분합니다. 우변에 $n+1$에 대한 정보가 있기 때문에 특정한 $\Psi^n_i$에 대해 다음 단계의 $\Psi^{n+1}_i$를 곧바로 계산할 수 없습니다. 대신 위의 식을 다음과 같이 변형할 수 있습니다: $$ \left(1 + \frac{2\kappa \Delta t}{\Delta x^2}\right)\Psi^{n+1}_i - \frac{\kappa \Delta t}{\Delta x^2}(\Psi^{n+1}_{i+1} + \Psi^{n+1}_{i-1}) = \Psi^n_i. $$ 모든 $1 \le i \le N - 1$에 대해 위의 식을 쓸 수 있고, $i=0$, $i=N$의 경우 $\Psi^{n+1}_i = \Psi^n_i$의 경계조건을 적용하겠습니다. 이제 연립방정식을 $\bm{A}\Psi^{n+1}=\Psi^n$으로 나타낼 수 있습니다. 여기서 $\bm{A}$는 다음과 같은 $(N+1)\times (N+1)$ 행렬입니다: $$ \bm{A}=\begin{pmatrix} 1 & 0 & 0 & 0 & 0\\ - \frac{\kappa \Delta t}{\Delta x^2} & 1 + \frac{2\kappa \Delta t}{\Delta x^2} & - \frac{\kappa \Delta t}{\Delta x^2} & 0 & 0\\ 0 & - \frac{\kappa \Delta t}{\Delta x^2} & 1 + \frac{2\kappa \Delta t}{\Delta x^2} & - \frac{\kappa \Delta t}{\Delta x^2} & 0 \\ & \ddots & \ddots & \ddots & \\ 0 & 0 & - \frac{\kappa \Delta t}{\Delta x^2} & 1 + \frac{2\kappa \Delta t}{\Delta x^2} & - \frac{\kappa \Delta t}{\Delta x^2} \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix}. $$ 따라서 각 시간 단계마다 위의 행렬 방정식을 풀어 새로운 $\Psi$를 얻는 과정을 반복합니다. 
for time_step in range(tN):
    A = np.zeros((N + 1, N + 1), dtype=np.complex128)
    A[0][0] = A[N][N] = 1
    for i in range(1, N):
        A[i][i] = 1 + 2 * kappa * dt / dx / dx
        A[i][i + 1] = A[i][i - 1] = - kappa * dt / dx / dx
    Psi = np.linalg.solve(A, Psi)
$\bm{A}$가 삼대각 행렬tridiagonal matrix임을 이용하면 더 빠르게 풀 수 있습니다. 여기서는 scipy의 solve_banded를 이용하였습니다. 
from scipy.linalg import solve_banded
for time_step in range(tN):
    A_band = np.zeros((3, N + 1), dtype=np.complex128)
    A_band[1][0] = A_band[1][N] = 1
    A_band[1][1:N] = 1 + 2 * kappa * dt / dx / dx
    A_band[0][2:] = - kappa * dt / dx / dx
    A_band[2][:N - 1] = - kappa * dt / dx / dx
    Psi = solve_banded((1, 1), A_band, Psi)
이제 수치적으로 얻은 해와 해석적 해를 비교해보겠습니다. 
plt.plot(x, np.abs(Psi) ** 2, label='numerical')
plt.plot(x, np.abs(Psi_sol) ** 2, label='exact')
다음 그림은 시간 간격 $\Delta t = 0.0001$로 $1000$번 적분하여 얻은 $|\Psi(x, 0.1)|^2$을 나타낸 것입니다. 해석적 해와 크게 차이를 보이지 않지만 시간 간격 또는 전체 시간을 증가시키면 더 큰 오차를 볼 수 있습니다. 
plt.plot(x, Psi.real, label='num_real')
plt.plot(x, Psi.imag, label='num_imag')
plt.plot(x, Psi_sol.real, label='exact_real')
plt.plot(x, Psi_sol.imag, label='exact_imag')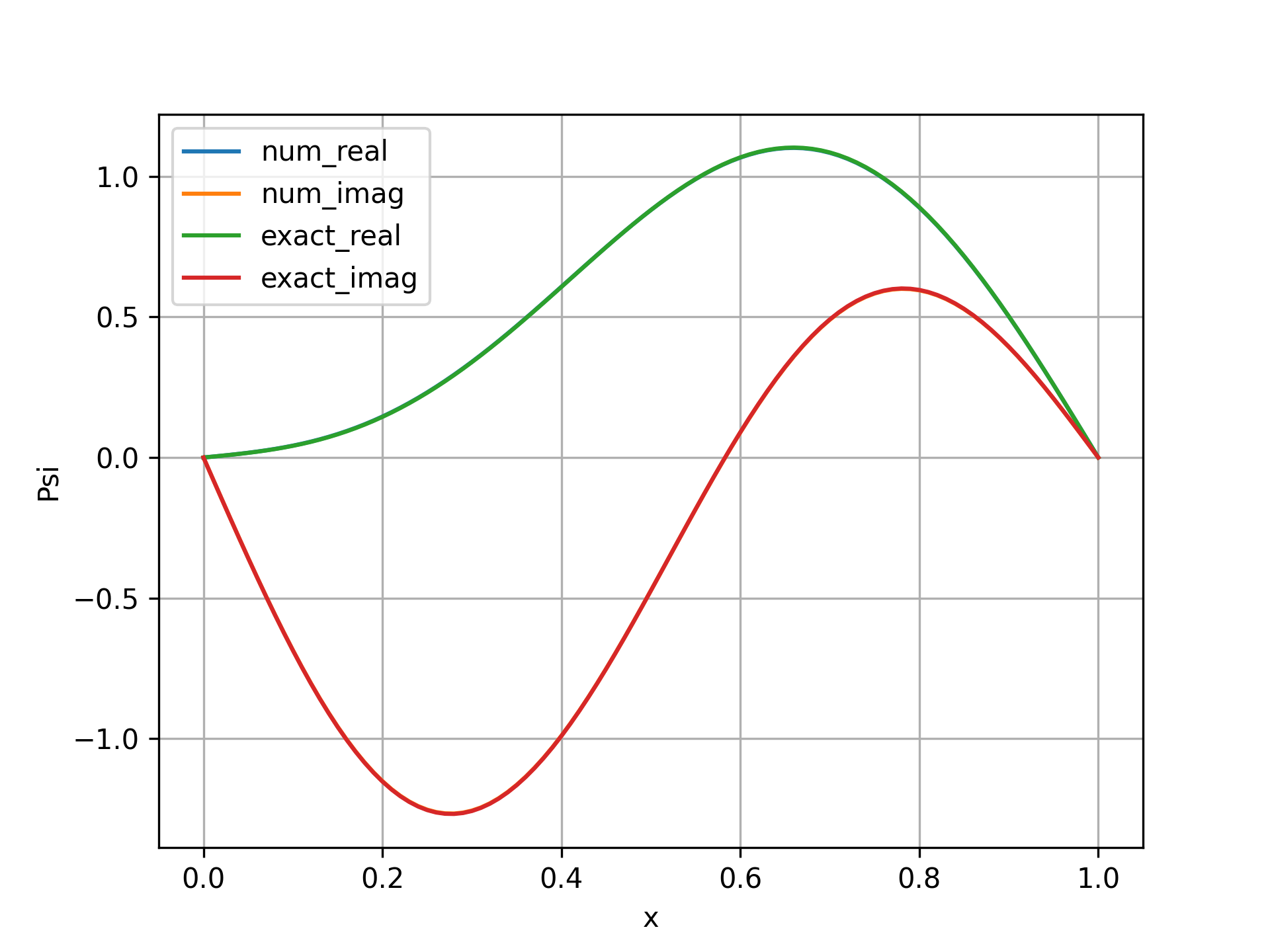
다음 그림은 위와 같은 과정으로 얻은 $\Psi(x, 0.1)$을 실수부와 허수부로 나누어 나타낸 것입니다. 다음 영상은 $n_1 = 1$, $n_2=2$일 때의 결과입니다. 다음 영상은 $n_1 = 2$, $n_2=3$일 때의 결과입니다. 다음 영상은 $n_1 = 3$, $n_2=7$일 때의 결과입니다.

Using Runge-Kutta Method

$4$차 정확도를 가지는 Runge-Kutta 방법을 사용하면 더 나은 결과를 얻을 수도 있습니다. 다음 영상은 위와 같이 $(n_1, n_2) = (2, 3), (3, 7)$일 때 4차 Runge-Kutta 방법을 사용한 결과입니다. 다음 영상은 $n_1 = 3$, $n_2=7$일 때의 결과입니다.